02. Linear Regression

본 글은 '모두를 위한 딥러닝 시즌 2'와 'pytorch로 시작하는 딥 러닝 입문'을 보며 공부한 내용을 정리한 글입니다.

필자의 의견이 섞여 들어가 부정확한 내용이 존재할 수 있습니다.

---

선형 회귀 = 학습 데이터와 가장 잘 맞는 하나의 직선을 찾는 과정!

0. 전체적인 학습 방법

(다른 학습에도 적용됨!)

1) 데이터에 적합한 가설을 설정한다.

2) cost function, 즉 오차비용 loss를 구할 함수를 결정한다.

3) 오차함수의 기울기를 이용해서 모델을 개선한다.(optimizer)

4) 만족스러운 결과가 나올 때 까지 3을 반복한다.

 

 

1. x가 하나인 linear regression 구현하기

1) Hypothesis

가설은 인공신경망의 구조를 나타낸다. 즉, 주어진 x에 대해 어떤 y를 뱉을 지 알려준다.

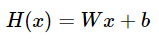
W = weight (가중치)

b = bias (편향)

 

 

2) 비용함수 계산

(비용 함수(cost function) = 손실 함수(loss function) = 오차 함수(error function) = 목적 함수(objective function))

 

MSE(Mean Squered Error, 평균 제곱 오차)를 이용해 계산.

쉽게 말해서, 각각의 오차의 제곱합에 대한 평균!

 

 

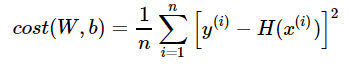
3) 최적화 optimizer

이 과정을 통해서 cost function의 값을 최소로 하는 W와 b를 찾는다.

그리고 W와 b를 찾아내는 과정을 '학습'이라고 한다.

 

여기서는 경사하강법, Gradient Descent를 이용해서 최적화한다. 즉, 기울기를 찾아서 기울기가 작아지는 쪽으로 움직이게 만든다.

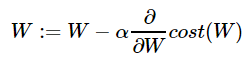
기울기가 음수일 때는 증가, 양수일 때엔 감소해야 한다.

 

💡 풀고자하는 각 문제에 따라 가설, 비용 함수, 옵티마이저는 전부 다를 수 있으며 선형 회귀에 가장 적합한 비용 함수는 평균 제곱 오차, 옵티마이저는 경사 하강법입니다.

 

3. full code

import torch
import torch.nn as nn #신경망 생성할 때 사용
import torch.nn.functional as F
import torch.optim as optim #가중치 갱신할 때 사용

# 데이터
x_train = torch.FloatTensor([[1], [2], [3]])
y_train = torch.FloatTensor([[2], [4], [6]])
# x는 입력값, y는 결과값
#x를 넣었을 때 y가 나오는 모델을 만들어야함.

# 모델 초기화
W = torch.zeros(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# requires_grad로 이 텐서가 학습될 수 있다고 명시.(자동 미분 가능)

# optimizer 설정
optimizer = optim.SGD([W, b], lr=0.01)

nb_epochs = 2900
for epoch in range(nb_epochs + 1):
    
    # H(x) 계산 - 가설 계산
    hypothesis = x_train * W + b
    
    # cost 계산 - 오차 비용! - 오차의 제곱근의 평균(MSE)
    cost = torch.mean((hypothesis - y_train) ** 2)

    # cost로 H(x) 개선
    optimizer.zero_grad() #gradient를 0으로 초기화(W, b가 업데이트 될 때 마다 미분값이 달라짐)
    cost.backward() #cost의 기울기를 구함
    optimizer.step() #w, b 업데이트

    # 100번마다 로그 출력
    if epoch % 100 == 0:
        print('Epoch {:4d}/{} W: {:.3f}, b: {:.3f} Cost: {:.6f}'.format(
            epoch, nb_epochs, W.item(), b.item(), cost.item()
        ))

 

 

---

<Reference>

https://deeplearningzerotoall.github.io/season2/lec_pytorch.html

https://wikidocs.net/53560