08. Perceptron

본 글은 '모두를 위한 딥러닝 시즌 2'와 'pytorch로 시작하는 딥 러닝 입문'을 보며 공부한 내용을 정리한 글입니다.

필자의 의견이 섞여 들어가 부정확한 내용이 존재할 수 있습니다.

---

0. 퍼셉트론 (Perceptron)

다수의 입력으로부터 하나의 결과를 내보내는 알고리즘. 뉴런의 동작 방식과 매우 유사하다.

 

각각의 입력 값에 가중치에 곱해서 y에 전달 된다. 이때, 전달된 값이 임계치를 노드가 활성화되고, 아니라면 활성화 되지 않는다. 이렇게 활성화를 결정하는 함수를 활성화 함수(active function)라고 하고, 그 종류에는 계단함수, 시그모이드, ReLU 등이 있다.

 

1. 단층 퍼셉트론

단층 퍼셉트론은 값을 보내는 단계과 값을 받아서 출력하는 두 단계로만 이루어졌다. 즉 입력층과 결과층으로만 이뤄진다. 층이 하나라 선형 영역에 대해서만 분류가 가능하다. 그래서 가능한 연산은 AND연산, OR연산, NAND연산이 있다. XOR 연산은 불가능 한데, 아래의 그래프를 보면 더 쉽게 이해가 가능하다.

AND GATE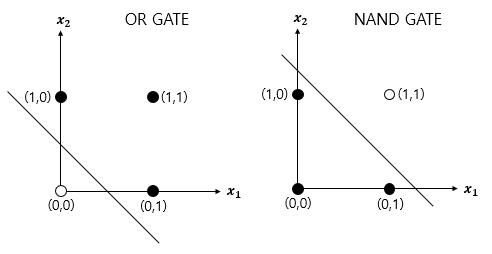

OR, NAND GATE

and, or, nand gate를 그려보면, 모두 직선 하나로 경우들을 분류할 수 있다.

 

XOR GATE

그러나, XOR gate는 직선 하나로는 분류를 할 수가 없다. 그러면 어떻게 해야 할까? 직선을 곡선으로 만들면 될까?

 

곡선으로 하니, 분류가 된다!

 

2. 다층 퍼셉트론

다층 퍼셉트론은 입력층, 출력층 외에 '은닉층(hidden layer)'이라는 또 다른 층이 있는 퍼셉트론을 의미한다. 다층 퍼셉트론에서는 XOR연산이 가능하다. Multylayer perceptron이라고도 하며, 줄여서 MLP 라고도 부른다.

 

 

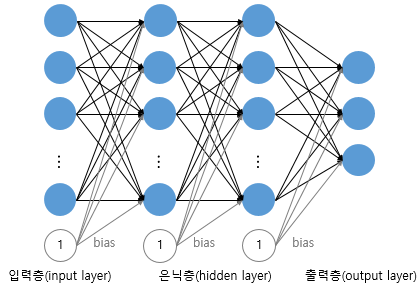
저렇게 은닉층이 2개 이상인 신경망을 심층 신경망(Deep Neural Network, DNN)라고 한다.

 

그런데 말입니다, 단일 퍼셉트론의 경우 오차를 바로바로 개선시킬 수 있다. (h(x) = xw + b 에서 w같은 경우, 바로바로 경사하강법을 적용했다) 그런데 다층 퍼셉트론의 경우, 각각의 가중치의 오차를 어떻게 개선할 수 있을까?

 

이제, 인공 신경망이 순전파 과정을 진행하여 예측값과 실제값의 오차를 계산하였을 때 어떻게 역전파 과정에서 경사 하강법을 사용하여 가중치를 업데이트하는지 알아보자. (인공 신경망의 학습은 오차를 최소화하는 가중치를 찾는 목적으로 순전파와 역전파를 반복하는 것을 말한다.)

 

3. 순전파 (Forward propagation)

입력층 -> 은닉층 -> 출력층 방향으로 향하면서, 값을 내어놓는 행위. 이 과정으로 알아낸 예측값으로 실제값과의 오차를 계산한다.

 

4. 역전파 (Backpropagation)

출력층 -> 은닉층 -> 입력층 방향으로 향하면서 가중치를 업데이트한다. 순전파를 통해 얻은 오차를 이용해서 가중치를 업데이트 하고 오차를 줄여나간다. 계산에는 미분의 연쇄법칙을 이용한다.

 

즉, 각각의 가중치들이 결과값에 영향을 미치는 비율(미분값)을 구한 뒤, 오차를 줄여나갈 수 있는 방향으로 빼 주는 것이다. 

 

결국 가중치에 대한 비용함수의 변화율 = 가중치에 대한 가설의 변화율 x 가설에 대한 활성화 함수의 변화율 x 활성화 함수에 대한 비용함수의 변화율이다. 여기에 미분의 연쇄법칙이 이용된다. (A에 대한 B 의 변화율 => B분의 A)

 

5.  XOR code (MLP)

import torch
 
device = 'cuda' if torch.cuda.is_available() else 'cpu'
 
# for reproducibility
torch.manual_seed(777)
if device == 'cuda':
    torch.cuda.manual_seed_all(777)
    
X = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]]).to(device)
Y = torch.FloatTensor([[0], [1], [1], [0]]).to(device)
 
#레이어 선언 (w와 b를 직접 설정)
# nn.Linear를 2개 사용한 것과 마찬가지
 
w1 = torch.Tensor(2, 2).to(device) # 2->2
b1 = torch.Tensor(2).to(device)
w2 = torch.Tensor(2, 1).to(device) #2->1
b2 = torch.Tensor(1).to(device)
 
################################## (추가된 부분)
torch.nn.init.normal_(w1)  #정규분포에서 가져온 값으로 텐서를 채운다.
torch.nn.init.normal_(b1)
torch.nn.init.normal_(w2)
torch.nn.init.normal_(b2)
###################################
 
def sigmoid(x):
    return 1.0/(1.0 + torch.exp(-x))
    
def sigmoid_prime(x): #시그모이드의 미분.
    return sigmoid(x)*(1-sigmoid(x))
    
learning_rate = 1
 
for step in range(10001):
    #forward
    l1 = torch.add(torch.matmul(X, w1), b1) #linear대로 계산(Wx + b)   (4*2)
    a1 = sigmoid(l1) #활성화
    l2 = torch.add(torch.matmul(a1, w2), b2) #(4*1)
    y_pred = sigmoid(l2) #활성화
    
    #BCE Loss사용
    cost = -torch.mean(Y * torch.log(y_pred) + (1 - Y) * torch.log(1 - y_pred))
    
    
    #back prop (chain rule)
    d_y_pred = (y_pred - Y)/(y_pred * (1.0 - y_pred) + 1e-7) #bce를 미분한 식
    
    #출력층 -> 은닉층
    d_l2 = d_y_pred * sigmoid_prime(l2) #(4*1)
    d_b2 = d_l2
    d_w2 = torch.matmul(torch.transpose(a1, 0, 1), d_b2) #(2*1)
    #a가 4*2라서 2*4로 바꿔서 행렬곱(2*4 x 4*1)을 할 수 있게 바꿔줌.
    
    #은닉층 -> 입력층
    d_a1 = torch.matmul(d_b2, torch.transpose(w2, 0, 1)) #(4*1) x (1*2) = (4*2)
    d_l1 = d_a1 * sigmoid_prime(l1) # 4*2
    d_b1 = d_l1 # 4*2
    d_w1 = torch.matmul(torch.transpose(X, 0, 1), d_b1) #(2*4) * (4*2) = (2*2)
    
    
    # weight update
    w1 = w1 - learning_rate * d_w1 #미분값(기울기)빼주기(방향이 중요!)
    b1 = b1 - learning_rate * torch.mean(d_b1, 0) 
    #편차는 스칼라인데 미분한 편차값이 벡터라서 맞춰줘야함??
    w2 = w2 - learning_rate * d_w2
    b2 = b2 - learning_rate * torch.mean(d_b2, 0)
    
    if step%100==0:
        print(step, cost.item())
        
        
l1 = torch.add(torch.matmul(X, w1), b1) #linear대로 계산(Wx + b)   (4*2)
a1 = sigmoid(l1) #활성화
l2 = torch.add(torch.matmul(a1, w2), b2) #(4*1)
y_pred = sigmoid(l2) #활성화
 
predicted = (y_pred > 0.5).float()
accuracy = (predicted == Y).float().mean()
    
    
print('Hypothesis:', y_pred.detach().cpu().numpy(), '\nCorrect: ', Y.detach().cpu().numpy(), '\nAccuracy: ', accuracy.item())

 

5-1.  XOR code (MLP) with nn.Module

import torch
 
device = 'cuda' if torch.cuda.is_available() else 'cpu'
 
# for reproducibility
torch.manual_seed(777)
if device == 'cuda':
    torch.cuda.manual_seed_all(777)
    
X = torch.FloatTensor([[0, 0], [0, 1], [1, 0], [1, 1]]).to(device)
Y = torch.FloatTensor([[0], [1], [1], [0]]).to(device)
 
# nn layers
linear1 = torch.nn.Linear(2, 10, bias=True)
linear2 = torch.nn.Linear(10, 10, bias=True)
linear3 = torch.nn.Linear(10, 10, bias=True)
linear4 = torch.nn.Linear(10, 1, bias=True)
sigmoid = torch.nn.Sigmoid()
 
# model
model = torch.nn.Sequential(linear1, sigmoid, linear2, sigmoid, linear3, sigmoid, linear4, sigmoid).to(device)
 
# define cost/loss & optimizer
criterion = torch.nn.BCELoss().to(device)
optimizer = torch.optim.SGD(model.parameters(), lr=3)  # modified learning rate from 0.1 to 1
 
for step in range(10001):
    optimizer.zero_grad()
    hypothesis = model(X)
 
    # cost/loss function
    cost = criterion(hypothesis, Y)
    cost.backward()
    optimizer.step()
 
    if step % 100 == 0:
        print(step, cost.item())
        
# Accuracy computation
# True if hypothesis>0.5 else False
with torch.no_grad():
    hypothesis = model(X)
    predicted = (hypothesis > 0.5).float()
    accuracy = (predicted == Y).float().mean()
    print('\nHypothesis: ', hypothesis.detach().cpu().numpy(), '\nCorrect: ', predicted.detach().cpu().numpy(), '\nAccuracy: ', accuracy.item())

 

 

<대충 정리하는 머신러닝 학습 과정>

1. 학습에 적합한 식을 가진 레이어 생성( n개)
2. model정의 (어떤순서로 돌리는지? 레이어 순서? + 활성화함수)
3. 비용함수와 최적화 함수 정의
4. 돌린다 (포워드 + 백워드)

 

---

<Reference>

https://deeplearningzerotoall.github.io/season2/lec_pytorch.html

https://wikidocs.net/60680

https://ko.wikipedia.org/wiki/%ED%8D%BC%EC%85%89%ED%8A%B8%EB%A1%A0

https://wikidocs.net/61010